Теория сложности и алгоритмы сокращения

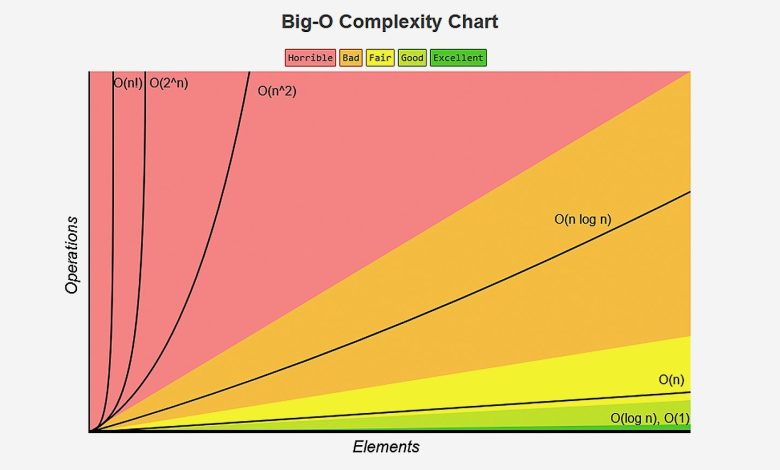
Теория сложности

Теория сложности в информатике изучает ресурсы, необходимые для выполнения вычислений. Она помогает оценить эффективность алгоритмов и предсказать их производительность в различных условиях. Одним из ключевых понятий в теории сложности является класс сложности, который определяет множество задач, решение которых возможно за определенное количество ресурсов.

Алгоритмы сокращения

Алгоритмы сокращения используются для сжатия данных с целью уменьшения объема информации, необходимого для их хранения или передачи. Существует множество методов сжатия данных, каждый из которых имеет свои преимущества и недостатки. Некоторые алгоритмы сокращения могут быть универсальными и применяться для различных типов данных, в то время как другие специализированы для определенных типов информации.

Примеры алгоритмов сокращения

Одним из наиболее популярных алгоритмов сокращения является алгоритм Хаффмана. Он основан на построении оптимального префиксного кода, который позволяет сократить количество бит, необходимых для представления символов в сообщении. Другим примером алгоритма сокращения является алгоритм Лемпеля-Зива, который используется для сжатия текстовых данных.

Применение алгоритмов сокращения

Алгоритмы сокращения широко применяются в компьютерной графике, сетевых технологиях, сжатии аудио и видео файлов, а также в области хранения данных. Они позволяют уменьшить объем информации, что в свою очередь снижает нагрузку на вычислительные системы и ускоряет передачу данных по сети. Эффективное использование алгоритмов сокращения позволяет экономить ресурсы и повышать производительность систем.